Swift Launch
Last week I launched Swift to two year groups at my school. The aim of this session was to demonstrate the power (and fun) of Swift Playgrounds, presenting the possibilities of Swift for mathematical discovery while emphasising the difference between experimentation and proof. We are very fortunate that every pupil at the school has their own iPad (with iOS 10 and hence access to Swift Playgrounds).
To begin we heard Conrad Wolfram’s take on the crisis in math education and I explained my vision of how Swift (“code in our hands”) can help bridge the gap between the classroom and the real world.
After introducing the group to the basics of Swift in “Learn to Code 1” through to using loops, I introduced Gauss’ famous sum, and in real time I wrote code (complete with typos and helpful red blob suggestions) as calculation. I showed how we could modify our code into a function using the beautiful idea of reversing the order of the numbers and pairing.
We then modified our loop to add odd numbers. It seems the sum of odd numbers yields a square. After checking a few more cases it soon became difficult to see if the sum was still a square, so we square-rooted (after importing the Foundation package). We could easily adapt our code to check the first 1000 cases, which indeed were all squares. A very believable conjecture is born from this, but the 1001st example could still fail. I then asked the class to study the “proof” diagram below, and explained how computing can guide our conjectures and help build up intuition but only proof is absolute.

I was very keen to demonstrate the scalability of Swift to the students, and so then shared heavily annotated code from WWDC 2016 which can control a robot from the iPad. I picked out the now familiar loop and functions, and then took charge of the SPRK+ robot. This created a real buzz in the room. The idea that we are doing “proper coding”, the language of Apps and Hackers, resonated.
To bring the session back to mathematics I shared one of the jewels of arithmetic, Euler’s formula, solving the Basel Problem, and giving a power series converging to Pi:
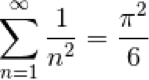
Hence,

Or, as a limit we can work with,
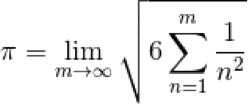
This was implemented using the code below. The “quick graph preview”, all within Playgrounds, gave a powerful and compelling visualisation of the asymptotic approach to Pi.