Autograd Package
Autograd can automatically differentiate native Python and Numpy code.
It integrates seemlessly with lots of Python’s features - loops, ifs, recursion and closures - and reapplying we get derivatives of derivatives of derivatives. It uses reverse-mode differentiation (formally, backpropagation), which means it efficiently takes gradients of scalar-valued functions with respect to array-valued arguments.
Autograd was written by Dougal Maclaurin, David Duvenaud and Matt Johnson, and is still being developed
The key method, from autograd import grad, will be useful to me in gradient-based optimization.
Example
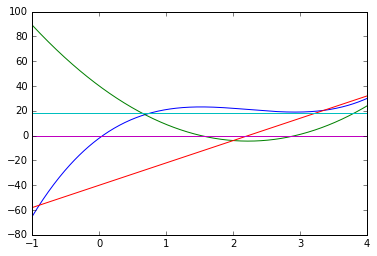
We can see grad in action by repeatedly differentiating a cubic and plotting the results on the same axes.
# Import packges I need
import autograd.numpy as np
from autograd import grad
# I begin by defining my function
def poly(x):
return 3*x**3-20*x**2+40*x-2
grad_poly = grad(poly) # Obtain its gradient function
grad_poly(1.0) # Evaluate the gradient at x = 1.0
9.0
Compare gradient of tangent with that of a small chord:
(poly(1.0001) - poly(0.9999)) / 0.0002
9.000000029981692
We can continue to differentiate as many times as we like:
def elementwise_grad(fun):
return grad(lambda x: np.sum(fun(x)))
grad_poly = elementwise_grad(poly)
grad_poly_2 = elementwise_grad(grad_poly) # second derivative
grad_poly_3 = elementwise_grad(grad_poly_2) # third derivative
grad_poly_4 = elementwise_grad(grad_poly_3) # fourth derivative
%matplotlib inline
import matplotlib.pyplot as plt
x = np.linspace(-1, 4, 500)
plt.plot(x, poly(x),
x, grad_poly(x),
x, grad_poly_2(x),
x, grad_poly_3(x),
x, grad_poly_4(x))
plt.show()